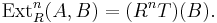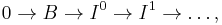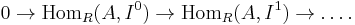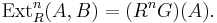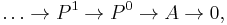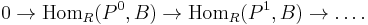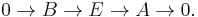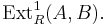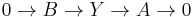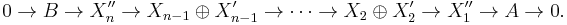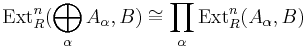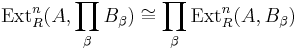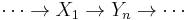Ext functor
In mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics.
Contents |
Definition and computation
Let  be a ring and let
be a ring and let 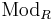 be the category of modules over R. Let
be the category of modules over R. Let  be in
be in 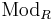 and set
and set 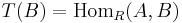 , for fixed
, for fixed  in
in 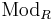 . This is a left exact functor and thus has right derived functors
. This is a left exact functor and thus has right derived functors 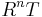 . The Ext functor is defined by
. The Ext functor is defined by
This can be calculated by taking any injective resolution
and computing
Then 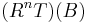 is the homology of this complex. Note that
is the homology of this complex. Note that 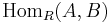 is excluded from the complex.
is excluded from the complex.
An alternative definition is given using the functor 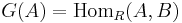 . For a fixed module B, this is a contravariant left exact functor, and thus we also have right derived functors
. For a fixed module B, this is a contravariant left exact functor, and thus we also have right derived functors 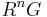 , and can define
, and can define
This can be calculated by choosing any projective resolution
and proceeding dually by computing
Then 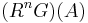 is the homology of this complex. Again note that
is the homology of this complex. Again note that 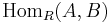 is excluded.
is excluded.
These two constructions turn out to yield isomorphic results, and so both may be used to calculate the Ext functor.
Ext and extensions
Equivalence of extensions
Ext functors derive their name from the relationship to extensions of modules. Given R-modules A and B, an extension of A by B is a short exact sequence of R-modules
Two extensions
are said to be equivalent (as extensions of A by B) if there is a commutative diagram
.
An extension of A by B is called split if it is equivalent to the trivial extension
There is a bijective correspondence between equivalence classes of extensions
of  by
by  and elements of
and elements of
The Baer sum of extensions
Given two extensions
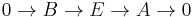 and
and 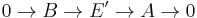
we can construct the Baer sum, by forming the pullback 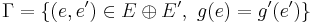 of
of 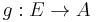 and
and 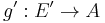 . We form the quotient
. We form the quotient  , that is we mod out by the relation
, that is we mod out by the relation 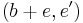 ~
~ 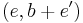 . The extension
. The extension
where the first arrow is ])](/2012-wikipedia_en_all_nopic_01_2012/I/e134919e6e8e48d2b9078228bf22f8ef.png) and the second
and the second ![[(e,e')] \mapsto g(e) (= g'(e'))](/2012-wikipedia_en_all_nopic_01_2012/I/072fb8f43b46bd02a3a01dd1ea88ae6d.png) thus formed is called the Baer sum of the extensions E and E'.
thus formed is called the Baer sum of the extensions E and E'.
Up to equivalence of extensions, the Baer sum is commutative and has the trivial extension as identity element. The extension 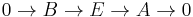 has for opposite the same extension with exactly one of the central arrows turned to their opposite eg the morphism g is replaced by -g.
has for opposite the same extension with exactly one of the central arrows turned to their opposite eg the morphism g is replaced by -g.
The set of extensions up to equivalence is an abelian group that is a realization of the functor 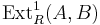
Construction of Ext in abelian categories
This identification enables us to define 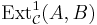 even for abelian categories
even for abelian categories 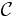 without reference to projectives and injectives. We simply take
without reference to projectives and injectives. We simply take 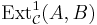 to be the set of equivalence classes of extensions of
to be the set of equivalence classes of extensions of  by
by  , forming an abelian group under the Baer sum. Similarly, we can define higher Ext groups
, forming an abelian group under the Baer sum. Similarly, we can define higher Ext groups 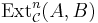 as equivalence classes of n-extensions
as equivalence classes of n-extensions
under the equivalence relation generated by the relation that identifies two extensions
 and
and
if there are maps 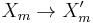 for all
for all  in
in 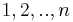 so that every resulting square commutes.
so that every resulting square commutes.
The Baer sum of the two n-extensions above is formed by letting 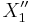 be the pullback of
be the pullback of 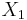 and
and 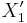 over
over  , and
, and 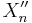 be the pushout of
be the pushout of 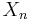 and
and 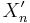 under
under  . Then we define the Baer sum of the extensions to be
. Then we define the Baer sum of the extensions to be
Further properties of Ext
The Ext functor exhibits some convenient properties, useful in computations.
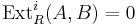 for
for 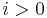 if either
if either  is injective or
is injective or  is projective.
is projective.
- A converse also holds: if
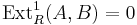 for all
for all  , then
, then 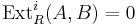 for all
for all  , and
, and  is injective; if
is injective; if 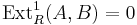 for all
for all  , then
, then 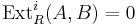 for all
for all  , and
, and  is projective.
is projective.
Ring structure and module structure on specific Exts
One more very useful way to view the Ext functor is this: when an element of 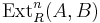 is considered as an equivalence class of maps
is considered as an equivalence class of maps 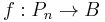 for a projective resolution
for a projective resolution 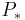 of
of  ; so, then we can pick a long exact sequence
; so, then we can pick a long exact sequence  ending with
ending with  and lift the map
and lift the map  using the projectivity of the modules
using the projectivity of the modules 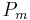 to a chain map
to a chain map 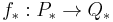 of degree -n. It turns out that homotopy classes of such chain maps correspond precisely to the equivalence classes in the definition of Ext above.
of degree -n. It turns out that homotopy classes of such chain maps correspond precisely to the equivalence classes in the definition of Ext above.
Under sufficiently nice circumstances, such as when the ring  is a group ring over a field
is a group ring over a field  , or an augmented
, or an augmented  -algebra, we can impose a ring structure on
-algebra, we can impose a ring structure on 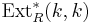 . The multiplication has quite a few equivalent interpretations, corresponding to different interpretations of the elements of
. The multiplication has quite a few equivalent interpretations, corresponding to different interpretations of the elements of 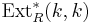 .
.
One interpretation is in terms of these homotopy classes of chain maps. Then the product of two elements is represented by the composition of the corresponding representatives. We can choose a single resolution of  , and do all the calculations inside
, and do all the calculations inside 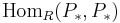 , which is a differential graded algebra, with cohomology precisely
, which is a differential graded algebra, with cohomology precisely 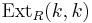 .
.
The Ext groups can also be interpreted in terms of exact sequences; this has the advantage that it does not rely on the existence of projective or injective modules. Then we take the viewpoint above that an element of 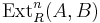 is a class, under a certain equivalence relation, of exact sequences of length
is a class, under a certain equivalence relation, of exact sequences of length 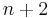 starting with
starting with  and ending with
and ending with  . This can then be spliced with an element in
. This can then be spliced with an element in 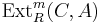 , by replacing
, by replacing
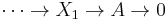 and
and 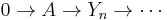
with
where the middle arrow is the composition of the functions 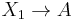 and
and 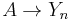 . This product is called the Yoneda splice.
. This product is called the Yoneda splice.
These viewpoints turn out to be equivalent whenever both make sense.
Using similar interpretations, we find that 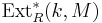 is a module over
is a module over 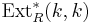 , again for sufficiently nice situations.
, again for sufficiently nice situations.
Interesting examples
If 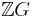 is the integral group ring for a group
is the integral group ring for a group  , then
, then 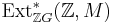 is the group cohomology
is the group cohomology 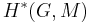 with coefficients in
with coefficients in  .
.
For 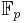 the finite field on
the finite field on  elements, we also have that
elements, we also have that 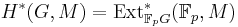 , and it turns out that the group cohomology doesn't depend on the base ring chosen.
, and it turns out that the group cohomology doesn't depend on the base ring chosen.
If  is a
is a  -algebra, then
-algebra, then 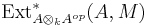 is the Hochschild cohomology
is the Hochschild cohomology 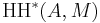 with coefficients in the A-bimodule M.
with coefficients in the A-bimodule M.
If  is chosen to be the universal enveloping algebra for a Lie algebra
is chosen to be the universal enveloping algebra for a Lie algebra 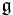 , then
, then 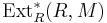 is the Lie algebra cohomology
is the Lie algebra cohomology 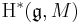 with coefficients in the module M.
with coefficients in the module M.
See also
- Tor functor
- The Grothendieck group is a construction centered on extensions
- The universal coefficient theorem for cohomology is one notable use of the Ext functor
References
- Gelfand, Sergei I.; Manin, Yuri Ivanovich (1999), Homological algebra, Berlin: Springer, ISBN 978-3-540-65378-3
- Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, ISBN 978-0-521-55987-4, OCLC 36131259, MR1269324